Fraktali - beskonačni oblici
Od samih malih nogu počinjemo da se zanimamo za oblike i uvek su opčinjavali čovečanstvo. Uostalom, kako da ne, kada su zadovoljstvo za oči? Osnovni su deo umetnosti, a i bilo čega što vidimo. Fraktali su možda najzanimljiviji među njima.
Po Benoi Mandelbrotu, fraktal je „geometrijski lik koji se može razložiti na manje delove tako da je svaki od njih, makar približno, umanjena kopija celine“. Za takve likove se kaže da su sami sebi slični. Ako je pri svakoj veličini fraktal istog oblika, onda je to afina samosličnost. Pored fraktala, takve su i obale, ali o njima će biti reči u nekom drugom članku. Pored samosličnosti, fraktale karakterišu i beskonačna složenost i dimenzionalnost.

Mandelbrotov skup, izvor: Vikimedija komons
Fraktalna dimenzija je odnos koji opisuje fraktalne obrasce ili skupove mereći njihovu složenost kao odnos promene u odnosu na promenu skale. Njima se opisuju mnogi predmeti i pojave, poput: turbulencije, rečnih sistema, urbanog razvoja, medicine i tržišnih trendova. Sama zamisao fraktalne dimenzije se može zapaziti još od 17. veka, mada se matematičaru i astronomu, Apoloniju iz Pergama, pripisuje da je uvideo da se beskonačno malih kružnica koje se dodiruju može upisati u jednu veću, dok je do izraza fraktal (od latinskog fractus, slomljen ili razlomljen) i fraktalna dimenzija došao Benoa Mandelbrot 1975.
Izuzetno jako zanimljiva osobina je da fraktalna dimenzija uopšte ne mora da bude prirodan broj, za razliku od euklidske geometrije. Najpre pomenimo kako se skaliraju konačne geometrijske figure: dupliranje ivice mnogougla daje četvorostruku površinu (što je 22), dupliranje poluprečnika sfere daje osmostruku zapreminu (što je 23). Međutim, kada se dužine jednodimenzionalnog fraktala sve dupliraju, prostorni sadržaj se skalira izložiocem koji nije obavezno ceo broj, nego je često veći od „uobičajene“ dimenzije. Taj izložilac je naša fraktalna dimenzija.
Sam koncept fraktalne dimenzije leži u neučestalim pogledima na skaliranje i dimenziju. Kada biste merili duž prvo jednim štapom neke dužine (I vrste), pa onda štapom trećine dužine prethodnog (II vrste), dobili ste duž dužine tri štapa II vrste. Analogno, kada biste štapovima kvadrat merili kvadratom jedne dužine (neka se i ovde zove I vrste), pa kvadratom čije su stranice triput manje, tj. ⅓ puta veće (neka se i ovde zove II vrste), dobili biste 9 kvadrata II vrste. Iz ovih primera bismo mogli da uočimo obrazac za dimenziju: 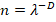 , gde je η broj mernih jedinica, λ faktor skaliranja, a D fraktalna dimenzija. Isto pravilo će se primenjivati u fraktalnoj geometriji, samo ne toliko očigledno. Fraktalna linija može biti izmerena prvo jedne dužine, ali novim štapom dužine trećine prethodnog može biti 4 dužine štapa, ne 3 kako bismo očekivali. Ovde će biti η = 4 kada je λ = ⅓, pa ćemo vrednost fraktalne dimenzije naći „preuređenjem“ naše gornje jednačine (logaritmovanjem):
, gde je η broj mernih jedinica, λ faktor skaliranja, a D fraktalna dimenzija. Isto pravilo će se primenjivati u fraktalnoj geometriji, samo ne toliko očigledno. Fraktalna linija može biti izmerena prvo jedne dužine, ali novim štapom dužine trećine prethodnog može biti 4 dužine štapa, ne 3 kako bismo očekivali. Ovde će biti η = 4 kada je λ = ⅓, pa ćemo vrednost fraktalne dimenzije naći „preuređenjem“ naše gornje jednačine (logaritmovanjem): 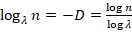 . U ovom slučaju, Kohove pahuljice, fraktalna dimenzija je D = 1.26186 ... Ova dimenzija se naziva Hausdorfova dimenzija, po matematičaru Feliksu Hausdorfu koji ju je uveo. Zbog zasluga u izračunavanju dimenzija izuzetno složenih i nepravilnih fraktala, neretko se zove i Hausdorf–Bezikovičeva dimenzija, po matematičaru Abramu Bezikoviču.
. U ovom slučaju, Kohove pahuljice, fraktalna dimenzija je D = 1.26186 ... Ova dimenzija se naziva Hausdorfova dimenzija, po matematičaru Feliksu Hausdorfu koji ju je uveo. Zbog zasluga u izračunavanju dimenzija izuzetno složenih i nepravilnih fraktala, neretko se zove i Hausdorf–Bezikovičeva dimenzija, po matematičaru Abramu Bezikoviču.
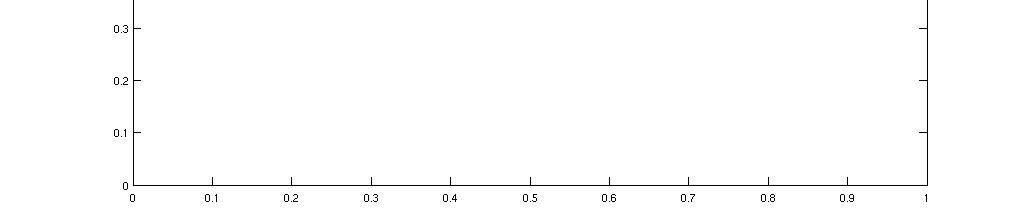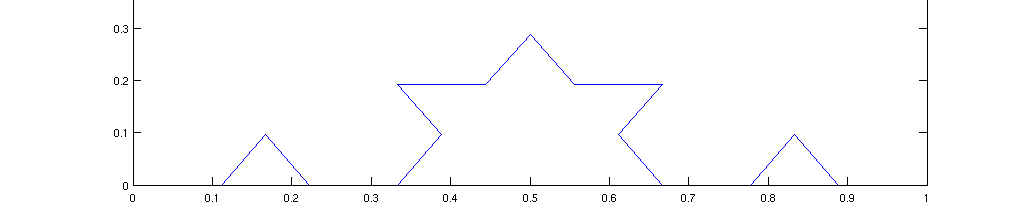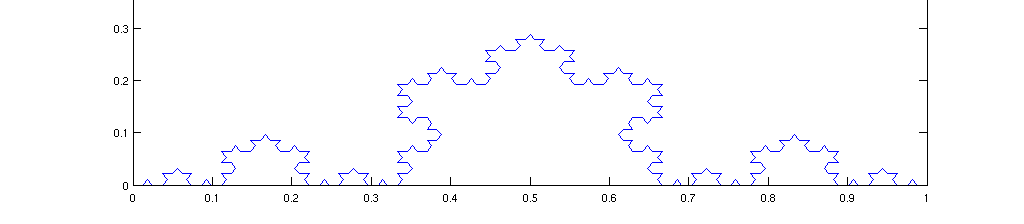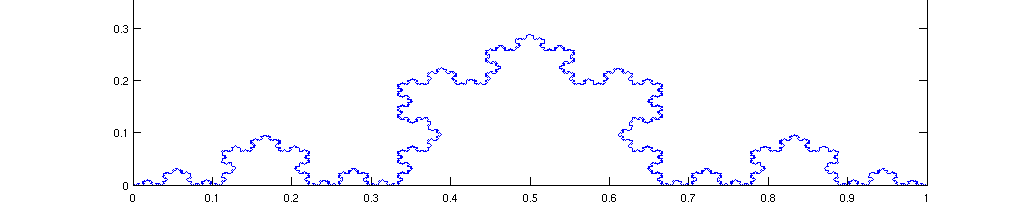
Animacija stvaranja Kohove pahuljice, izvor: Vikimedija komons
Gotfrid Lajbnic se bavio fraktalima i posmatrao rekurzivnu samosličnost. Koristio je izraz „razlomljeni izložilac“ odnoseći se na osobinu skaliranja. Doduše, on je smatrao i pravu fraktalom, što po savremenoj misli nije fraktal, jer izostaje beskonačna složenost. Dalje zanimanje za fraktale opada narednih 200 godina, dok ono malo matematičara koji su se bavili njima ih je nazivalo „matematičkim čudovištima“.
18. jula 1872, na Kraljevskoj pruskoj akademiji nauka, Karl Vajerštras je otkrio posebnu funkciju koju sada poznajemo pod njegovim prezimenom. Ova funkcija je neprekidna u svakoj tački, ali nije diferencijabilna ni u jednoj tački. Njegov student, Georg Kantor, prisustvovao je njegovim predavanjima i kasnije i sam postao matematičar. On se bavio odsečcima realne prave koje danas zovemo Kantor skup. Ove duži su samoslične i prate obrazac izbacujući intervale. Kantorov skup se smatra fraktalom danas.
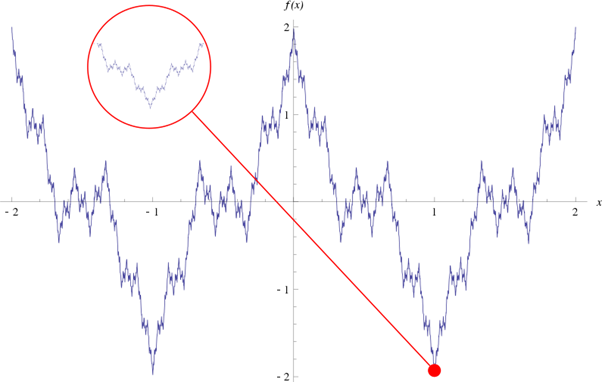
Vajerštrasova funkcija i prikaz samosličnosti, izvor: Vikimedija komons
Helgeu fon Kohu se 1904. godine nije svidela Vajerštrasova definicija da su fraktali neprekidni, ali ne diferencijabilni. On je počeo s idejama Poenkarea (matematičara) i predložio definiciju iz geometrije. Rukom je crtao identični ponavljajući obrazac nama danas poznat kao Kohova pahuljica.
Godine 1915, Vaclav Sjerpinjski je napravio trougao Sjerpinjskog, a 1916. je nastao tepih Sjerpinjskog.

Trougao Sjerpinjskog, izvor: Vikimedija komons
Koju godinu kasnije, počela je ozbiljnije da se istražuje kompleksna dinamika, pre svega u radovima Pjera Fatua i Gastona Žulije, francuskih matematičara. Konkretno, došli su do polja koje zovemo teorija haosa. Došli su do skoro identičnih iterativnih funkcija i kompleksnih brojeva. Nažalost, istraživanja fraktala su bila ograničena dotadašnjom tehnologijom, iako se neki mogu ručno nacrtati (poput gorepomenute Kohove pahuljice).
Pomenuti Benoa Mandelbrot je koristio štampače za svoja izučavanja, međutim, kada se dovoljno razvila računarska grafika, počeo je i nju da koristi za izučavanja fraktala. Mandelbrot je koristio ideje fraktala da izučava fizičke objekte, verovatnoću, ponašanje na berzama i dinamiku.
Računarski grafičar, Loren Karpenter, napravio je softver 1980. godine koji obrađuje i vizualizuje krajolike ispunjene fraktalima. Ovakav metod se i danas koristi za stvaranje realističnih krajolika u video-igricama.
Fraktalna matematika ima mnogobrojne primene. Koristi se za izučavanje teorije haosa i kompleksnih dinamičkih sistema, stvaranje zapanjujućih računarskih slika, izučavanje arhitekture internet mreža, pa čak i davanje dijagnoze brojnih bolesti. Fraktalna geometrija i Hausdorfova dimenzija prikupljenih podataka se mogu koristiti da se shvati složenost sistema i oblika i čak, na razne načine, mogu da opišu nepredvidive fenomene. Fraktali su jako česti u umetnosti, s tim da se danas stvaraju mahom medijskom umetnošću i programima koje možete naći čak i besplatne i sami se pozabaviti njima. Fraktala ima u biologiji, poput krvnih zrnaca (čiji obrascu omogućuju doktorima davanje bolje terapije pacijentima), nervnih sistema mnogih životinja i rasta bakterija, u cveću i biljkama (salata, brokoli, ananas), spirale rasta, gromovi, respiratorni sistem. Fraktala ima i u geografiji: reke i reljef. Možda neočekivano, ali su poprilično primenjeni u tehnologiji: fraktalne antene (omogućuju rad telefona na više frekvencija), fraktalni tranzistori (deluju na širem opsegu bez gubitaka u performansama u telefonima, mikrotalasnima i televizorima), procesovanjima signala i mnogi drugi.
